29 M9A: Basic Regression
This content draws on material from Statistical Inference via Data Science: A ModernDive into R and the Tidyverse by Chester Ismay and Albert Y. Kim, licensed under CC BY-NC-SA 4.0
Changes to the source material include addition of new material; light editing; rearranging, removing, and combining original material; adding and changing links; and adding first-person language from current author.
The resulting content is licensed under CC BY-NC-SA 4.0.
29.1 Introduction
Now that we are equipped with skills for wrangling, tidying, and visualizing data, let’s proceed with data modeling. As I stated at the end of this week’s understanding reading, this walkthrough is going to repeat much of what we read there, though this focus on modeling—and practical application of data science—will give us a new way of thinking about it.
The fundamental premise of data modeling is to make explicit the relationship between:
- an outcome variable , also called a dependent variable or response variable, and
- an explanatory variable , also called a predictor variable, an independent variable, or a covariate.
Another way to state this is using mathematical terminology: we will model the outcome variable “as a function” of the explanatory/predictor variable . When I say “function” here, I’m no referring to functions in R like the ggplot() function, but rather as a mathematical function.
Why do we refer to the variable as both an explanatory variable and a predictor variable? That’s because even though the two terms are often used interchangeably, data modeling serves (roughly speaking) one of two purposes:
- Modeling for explanation: When you want to explicitly describe and quantify the relationship between the outcome variable and a set of explanatory variables , determine the significance of any relationships, have measures summarizing these relationships, and possibly identify any causal relationships between the variables. Causal here refers to a cause-effect relationship; we’re interested in whether a change in one variable causes a change in another variable.
- Modeling for prediction: When you want to predict an outcome variable based on the information contained in a set of predictor variables . Unlike modeling for explanation, however, you don’t care so much about understanding how all the variables relate and interact with one another, but rather only whether you can make good predictions about using the information in .
For example, say you are interested in an outcome variable of whether patients develop lung cancer and information on their risk factors, such as smoking habits, age, and socioeconomic status. If we are modeling for explanation, we would be interested in both describing and quantifying the effects of the different risk factors. One reason could be that you want to design an intervention to reduce lung cancer incidence in a population, such as targeting smokers of a specific age group with advertising for smoking cessation programs. If we are modeling for prediction, however, we wouldn’t care so much about understanding how all the individual risk factors contribute to lung cancer, but rather only whether we can make good predictions of which people will contract lung cancer.
In this book, we’ll focus on modeling for explanation and hence refer to as explanatory variables. If you are interested in learning about modeling for prediction, you can check out books and courses on the field of machine learning such as An Introduction to Statistical Learning with Applications in R (ISLR) (James et al., 2017). Furthermore, while there exist many techniques for modeling, such as tree-based models and neural networks, in this book we’ll focus on one particular technique: linear regression. Linear regression is one of the most commonly-used and easy-to-understand approaches to modeling.
Linear regression involves a numerical outcome variable and explanatory variables that are either numerical or categorical. Furthermore, the relationship between and is assumed to be linear, or in other words, a line. However, we’ll see that what constitutes a “line” will vary depending on the nature of your explanatory variables .
In Chapter 29 on basic regression, we’ll only consider models with a single explanatory variable . In Section 29.2, the explanatory variable will be numerical. This scenario is known as simple linear regression. In Section 29.3, the explanatory variable will be categorical.
In Chapter 32 on multiple regression, we’ll extend the ideas behind basic regression and consider models with two explanatory variables and . In Section 32.2, we’ll have two numerical explanatory variables. In Section 32.3, we’ll have one numerical and one categorical explanatory variable. In particular, we’ll consider two such models: interaction and parallel slopes models.
In Chapter 44 on inference for regression, we’ll revisit our regression models and analyze the results using the tools for statistical inference you’ll develop in Chapters 35, 38, and 41 on sampling, confidence intervals, and hypothesis testing and -values, respectively.
Let’s now begin with basic regression, which refers to linear regression models with a single explanatory variable . We’ll also discuss important statistical concepts like the correlation coefficient, that “correlation isn’t necessarily causation,” and what it means for a line to be “best-fitting.”
Needed packages
Let’s now load all the packages needed for this chapter (this assumes you’ve already installed them). It’s worth reviewing these packages in particular:
- The
tidyverse“umbrella” package. Recall from our discussion in Section 20.4 that loading thetidyversepackage by runninglibrary(tidyverse)loads the following commonly used data science packages all at once:ggplot2for data visualizationdplyrfor data wranglingtidyrfor converting data to “tidy” formatreadrfor importing spreadsheet data into R- As well as the more advanced
purrr,tibble,stringr, andforcatspackages
- The
moderndivepackage of datasets and functions for tidyverse-friendly introductory linear regression. - The
skimrpackage, which provides a simple-to-use function to quickly compute a wide array of commonly used summary statistics.
If needed, read Section 8.4 for information on how to install and load R packages.
29.2 One numerical explanatory variable
Why do some professors and instructors at universities and colleges receive high teaching evaluations scores from students while others receive lower ones? Are there differences in teaching evaluations between instructors of different demographic groups? Could there be an impact due to student biases? These are all questions that are of interest to university/college administrators, as teaching evaluations are among the many criteria considered in determining which instructors and professors get promoted.
Researchers at the University of Texas in Austin, Texas (UT Austin) tried to answer the following research question: what factors explain differences in instructor teaching evaluation scores? To this end, they collected instructor and course information on 463 courses. A full description of the study can be found at openintro.org.
In this section, we’ll keep things simple for now and try to explain differences in instructor teaching scores as a function of one numerical variable: the instructor’s “beauty” score (we’ll see how this score was determined shortly). Could it be that instructors with higher “beauty” scores also have higher teaching evaluations? Could it be instead that instructors with higher “beauty” scores tend to have lower teaching evaluations? Or could it be that there is no relationship between “beauty” score and teaching evaluations? We’ll answer these questions by modeling the relationship between teaching scores and “beauty” scores using simple linear regression where we have:
- a numerical outcome variable (the instructor’s teaching score) and
- a single numerical explanatory variable (the instructor’s “beauty” score).
29.2.1 Exploratory data analysis
The data on the 463 courses at UT Austin can be found in the evals data frame included in the moderndive package. However, to keep things simple, let’s select() only the subset of the variables we’ll consider in this chapter, and save this data in a new data frame called evals_walkthrough:
A crucial step before doing any kind of analysis or modeling is performing an exploratory data analysis, or EDA for short. EDA gives you a sense of the distributions of the individual variables in your data, whether any potential relationships exist between variables, whether there are outliers and/or missing values, and (most importantly) how to build your model. Here are three common steps in an EDA:
- Most crucially, looking at the raw data values.
- Computing summary statistics, such as means, medians, and interquartile ranges.
- Creating data visualizations.
Let’s perform the first common step in an exploratory data analysis: looking at the raw data values. Because this step seems so trivial, unfortunately many data analysts ignore it. However, getting an early sense of what your raw data looks like can often prevent many larger issues down the road.
You can do this by using RStudio’s spreadsheet viewer or by using the glimpse() function as introduced in Subsection 8.5.3 on exploring data frames:
Rows: 463
Columns: 4
$ ID <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,…
$ score <dbl> 4.7, 4.1, 3.9, 4.8, 4.6, 4.3, 2.8, 4.1, 3.4, 4.5, 3.8, 4.5, 4.…
$ bty_avg <dbl> 5.00, 5.00, 5.00, 5.00, 3.00, 3.00, 3.00, 3.33, 3.33, 3.17, 3.…
$ age <int> 36, 36, 36, 36, 59, 59, 59, 51, 51, 40, 40, 40, 40, 40, 40, 40…Observe that Rows: 463 indicates that there are 463 rows/observations in evals_walkthrough, where each row corresponds to one observed course at UT Austin. It is important to note that the observational unit is an individual course and not an individual instructor. Recall from Subsection 8.5.3 that the observational unit is the “type of thing” that is being measured by our variables. Since instructors teach more than one course in an academic year, the same instructor will appear more than once in the data. Hence there are fewer than 463 unique instructors being represented in evals_walkthrough. We’ll revisit this idea in Section 44.4, when we talk about the “independence assumption” for inference for regression.
A full description of all the variables included in evals can be found at openintro.org or by reading the associated help file (that is, by running ?evals in the console). However, let’s fully describe only the 4 variables we selected in evals_walkthrough:
ID: An identification variable used to distinguish between the 1 through 463 courses in the dataset.score: A numerical variable of the course instructor’s average teaching score, where the average is computed from the evaluation scores from all students in that course. Teaching scores of 1 are lowest and 5 are highest. This is the outcome variable of interest.bty_avg: A numerical variable of the course instructor’s average “beauty” score, where the average is computed from a separate panel of six students. “Beauty” scores of 1 are lowest and 10 are highest. This is the explanatory variable of interest.age: A numerical variable of the course instructor’s age. This is another explanatory variable that we could use to further examine the data.
An alternative way to look at the raw data values is by choosing a random sample of the rows in evals_walkthrough by piping it into the sample_n() function from the dplyr package. Here we set the size argument to be 5, indicating that we want a random sample of 5 rows. You can see my results in Table 29.1, but due to the random nature of the sampling, you will almost certainly end up with a different subset of 5 rows.
| ID | score | bty_avg | age |
|---|---|---|---|
| 129 | 3.7 | 3.00 | 62 |
| 109 | 4.7 | 4.33 | 46 |
| 28 | 4.8 | 5.50 | 62 |
| 434 | 2.8 | 2.00 | 62 |
| 330 | 4.0 | 2.33 | 64 |
Now that we’ve looked at the raw values in our evals_walkthrough data frame and got a preliminary sense of the data, let’s move on to the next common step in an exploratory data analysis: computing summary statistics. Let’s start by computing the mean and median of our numerical outcome variable score and our numerical explanatory variable “beauty” score denoted as bty_avg. We’ll do this by using the summarize() function from dplyr along with the mean() and median() summary functions we saw in Section 26.2.
evals_walkthrough %>%
summarize(mean_bty_avg = mean(bty_avg), mean_score = mean(score),
median_bty_avg = median(bty_avg), median_score = median(score))# A tibble: 1 × 4
mean_bty_avg mean_score median_bty_avg median_score
<dbl> <dbl> <dbl> <dbl>
1 4.41784 4.17473 4.333 4.3However, what if we want other summary statistics as well, such as the standard deviation (a measure of spread), the minimum and maximum values, and various percentiles?
Typing out all these summary statistic functions in summarize() would be long and tedious. Instead, let’s use the convenient skim() function from the skimr package. This function takes in a data frame, “skims” it, and returns commonly used summary statistics. Let’s take our evals_walkthrough data frame, select() only the outcome and explanatory variables teaching score and bty_avg, and pipe them into the skim() function:
| Name | Piped data |
| Number of rows | 463 |
| Number of columns | 2 |
| _______________________ | |
| Column type frequency: | |
| numeric | 2 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| score | 0 | 1 | 4.17 | 0.54 | 2.30 | 3.80 | 4.30 | 4.6 | 5.00 | ▁▁▅▇▇ |
| bty_avg | 0 | 1 | 4.42 | 1.53 | 1.67 | 3.17 | 4.33 | 5.5 | 8.17 | ▃▇▇▃▂ |
Note that I’ve prettified my output a bit here; yours ought to have the same values but look a bit different; don’t be surprised if I continue to do this with future output!
For the numerical variables teaching score and bty_avg it returns:
n_missing: the number of missing valuescomplete_rate: the proportion of non-missing or complete values (here, it’s 1, which is equivalent to 100%—nothing’s missing!)n: the total number of valuesmean: the averagesd: the standard deviationp0: the 0th percentile: the value at which 0% of observations are smaller than it (the minimum value)p25: the 25th percentile: the value at which 25% of observations are smaller than it (the 1st quartile)p50: the 50th percentile: the value at which 50% of observations are smaller than it (the 2nd quartile and more commonly called the median)p75: the 75th percentile: the value at which 75% of observations are smaller than it (the 3rd quartile)p100: the 100th percentile: the value at which 100% of observations are smaller than it (the maximum value)
Looking at this output, we can see how the values of both variables distribute. For example, the mean teaching score was 4.17 out of 5, whereas the mean “beauty” score was 4.42 out of 10. Furthermore, the middle 50% of teaching scores was between 3.80 and 4.6 (the first and third quartiles), whereas the middle 50% of “beauty” scores falls within 3.17 to 5.5 out of 10.
The skim() function only returns what are known as univariate summary statistics: functions that take a single variable and return some numerical summary of that variable. However, there also exist bivariate summary statistics: functions that take in two variables and return some summary of those two variables. In particular, when the two variables are numerical, we can compute the correlation coefficient. Generally speaking, coefficients are quantitative expressions of a specific phenomenon. A correlation coefficient is a quantitative expression of the strength of the linear relationship between two numerical variables. Its value ranges between -1 and 1 where:
- -1 indicates a perfect negative relationship: As one variable increases, the value of the other variable tends to go down, following a straight line.
- 0 indicates no relationship: The values of both variables go up/down independently of each other.
- +1 indicates a perfect positive relationship: As the value of one variable goes up, the value of the other variable tends to go up as well in a linear fashion.
Figure 29.1 gives examples of 9 different correlation coefficient values for hypothetical numerical variables and . For example, observe in the top right plot that for a correlation coefficient of -0.75 there is a negative linear relationship between and , but it is not as strong as the negative linear relationship between and when the correlation coefficient is -0.9 or -1.
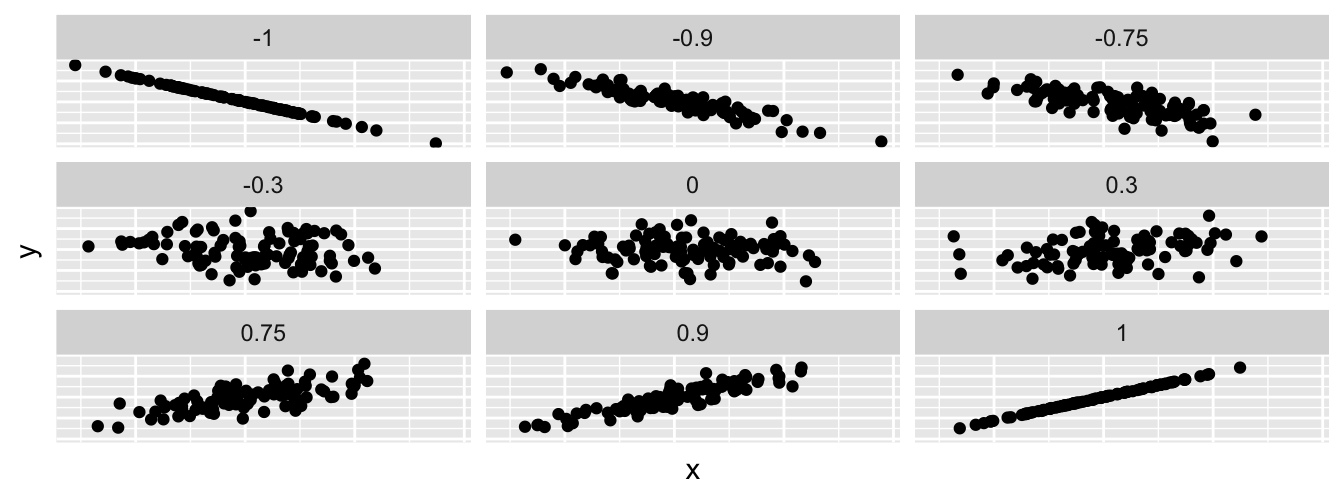
Figure 29.1: Nine different correlation coefficients.
The correlation coefficient can be computed using the get_correlation() function in the moderndive package. In this case, the inputs to the function are the two numerical variables for which we want to calculate the correlation coefficient.
We put the name of the outcome variable on the left-hand side of the ~ “tilde” sign, while putting the name of the explanatory variable on the right-hand side. This is known as R’s formula notation. We will use this same “formula” syntax with regression later in this chapter.
# A tibble: 1 × 1
cor
<dbl>
1 0.187142An alternative way to compute correlation is to use the cor() summary function within a summarize():
# A tibble: 1 × 1
correlation
<dbl>
1 0.187142In our case, the correlation coefficient of 0.187 indicates that the relationship between teaching evaluation score and “beauty” average is “weakly positive.” There is a certain amount of subjectivity in interpreting correlation coefficients, especially those that aren’t close to the extreme values of -1, 0, and 1. To develop your intuition about correlation coefficients, you can play the “Guess the Correlation” 1980s style video game found at https://www.guessthecorrelation.com/.
Figure 29.2: Preview of “Guess the Correlation” game.
Let’s now perform the last of the steps in an exploratory data analysis: creating data visualizations. Since both the score and bty_avg variables are numerical, a scatterplot is an appropriate graph to visualize this data. Let’s do this using geom_point() and display the result in Figure 29.3. Furthermore, in my version, I’ll highlight the six points in the top right of the visualization in a box.
ggplot(evals_walkthrough, aes(x = bty_avg, y = score)) +
geom_point() +
labs(x = "Beauty Score",
y = "Teaching Score",
title = "Scatterplot of relationship of teaching and beauty scores")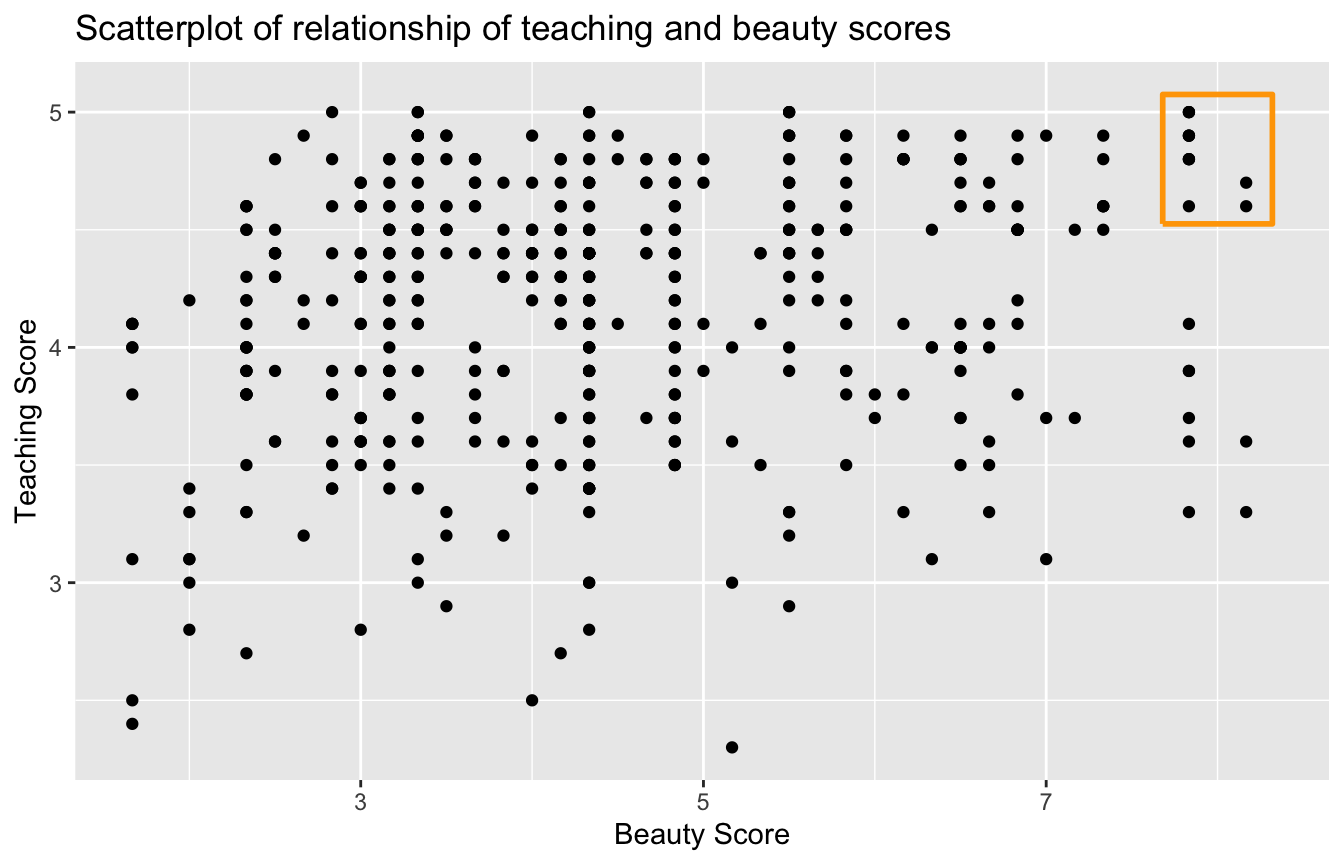
Figure 29.3: Instructor evaluation scores at UT Austin.
Observe that most “beauty” scores lie between 2 and 8, while most teaching scores lie between 3 and 5. Furthermore, while opinions may vary, I’d describe the relationship between teaching score and “beauty” score is “weakly positive.” This is consistent with our earlier computed correlation coefficient of 0.187.
Furthermore, there appear to be six points in the top-right of this plot highlighted in the box. However, this is not actually the case, as this plot suffers from overplotting. Recall from Subsection 23.4.2 that overplotting occurs when several points are stacked directly on top of each other, making it difficult to distinguish them. So while it may appear that there are only six points in the box, there are actually more. This fact is only apparent when using geom_jitter() in place of geom_point(); to help you see this, I’ll once again use the same small box in my version of the plot (Figure 29.4).
ggplot(evals_walkthrough, aes(x = bty_avg, y = score)) +
geom_jitter() +
labs(x = "Beauty Score", y = "Teaching Score",
title = "Scatterplot of relationship of teaching and beauty scores")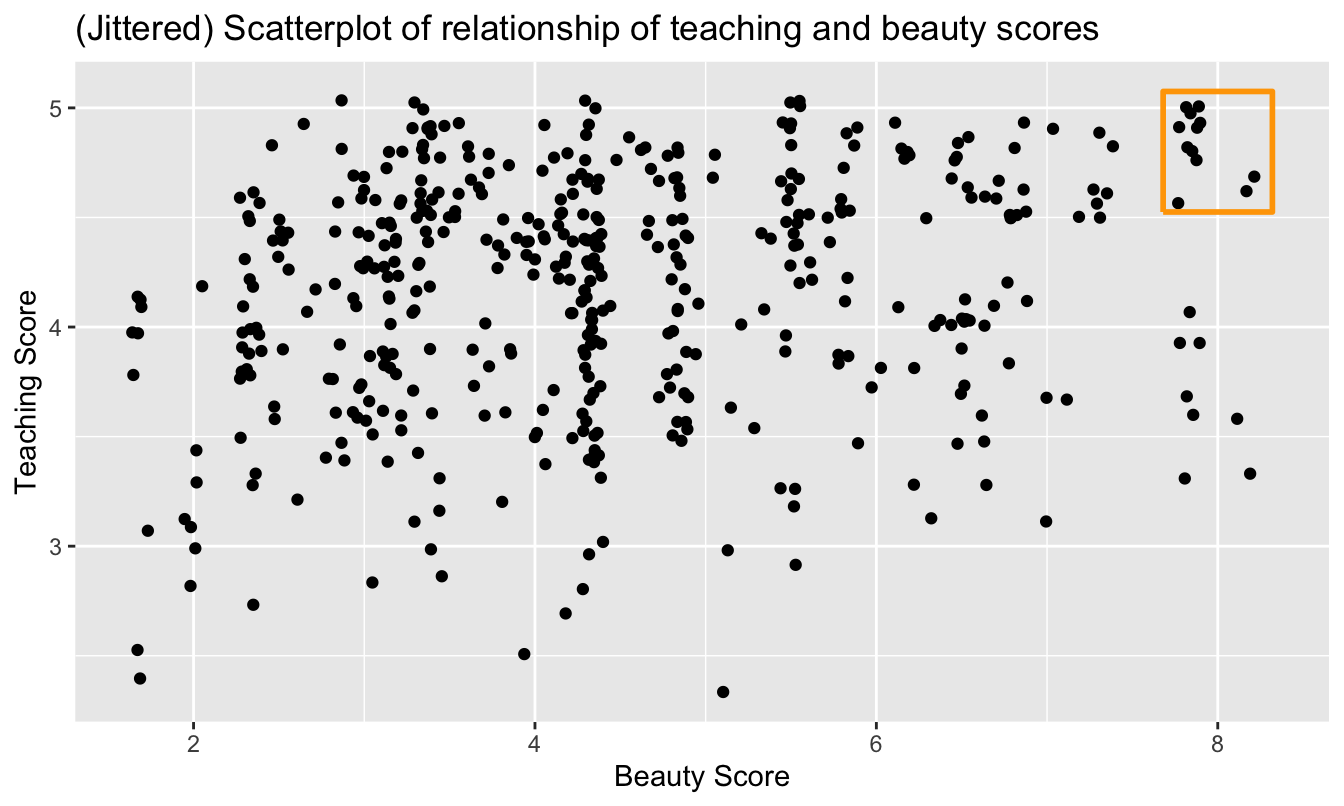
Figure 29.4: Instructor evaluation scores at UT Austin.
It is now apparent that there are 12 points in the area highlighted in the box and not six as originally suggested in Figure 29.3. Recall from Subsection 23.4.2 on overplotting that jittering adds a little random “nudge” to each of the points to break up these ties. Furthermore, recall that jittering is strictly a visualization tool; it does not alter the original values in the data frame evals_walkthrough. To keep things simple going forward, however, I’ll only present regular scatterplots rather than their jittered counterparts.
Let’s build on the unjittered scatterplot in Figure 29.3 by adding a “best-fitting” line: of all possible lines we can draw on this scatterplot, it is the line that “best” fits through the cloud of points. We do this by adding a new geom_smooth(method = "lm", se = FALSE) layer to the ggplot() code that created the scatterplot in Figure 29.3. The method = "lm" argument sets the line to be a “linear model.” The se = FALSE argument suppresses standard error uncertainty bars. (We’ll explore the concept of standard error later in Subsection 35.4.2.)
ggplot(evals_walkthrough, aes(x = bty_avg, y = score)) +
geom_point() +
labs(x = "Beauty Score", y = "Teaching Score",
title = "Relationship between teaching and beauty scores") +
geom_smooth(method = "lm", se = FALSE)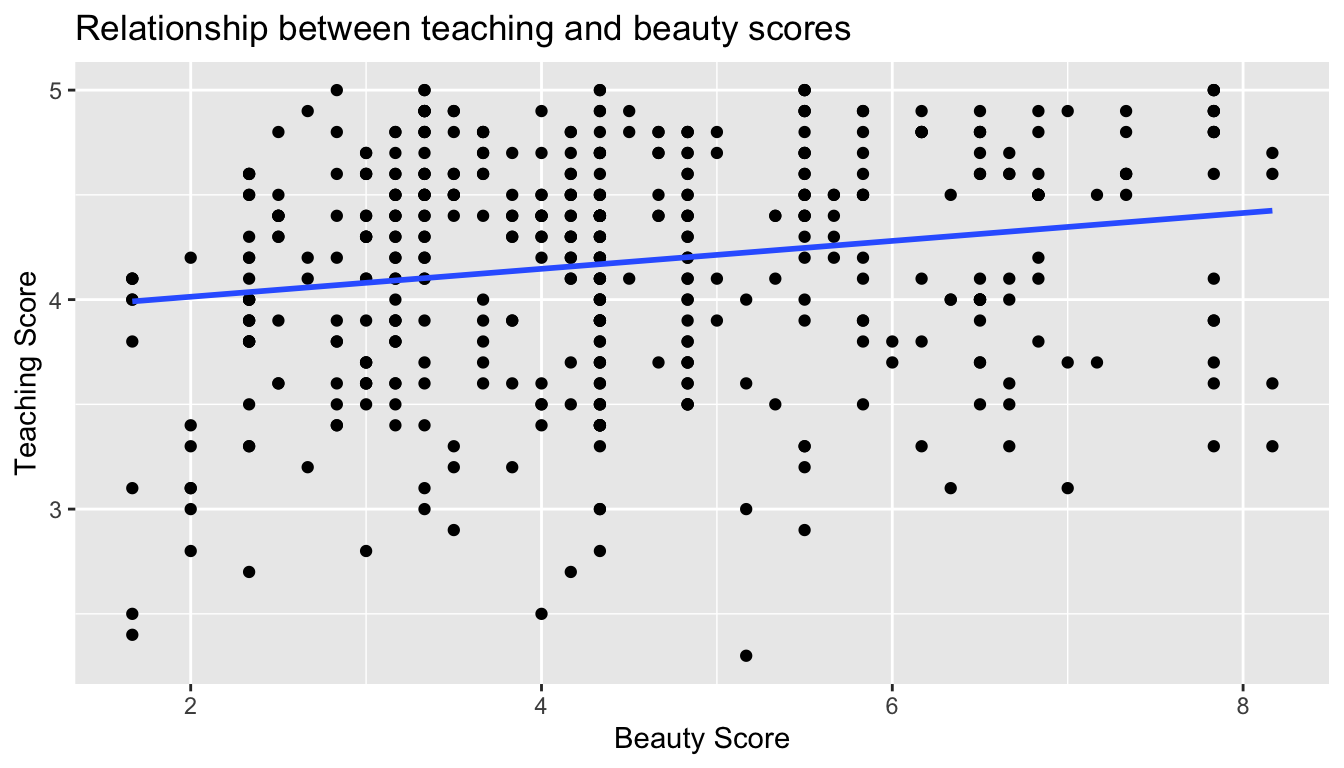
Figure 29.5: Regression line.
The line in the resulting Figure 29.5 is called a “regression line.” The regression line is a visual summary of the relationship between two numerical variables, in our case the outcome variable score and the explanatory variable bty_avg. The positive slope of the blue line is consistent with our earlier observed correlation coefficient of 0.187 suggesting that there is a positive relationship between these two variables: as instructors have higher “beauty” scores, so also do they receive higher teaching evaluations. We’ll see later, however, that while the correlation coefficient and the slope of a regression line always have the same sign (positive or negative), they typically do not have the same value.
Furthermore, a regression line is “best-fitting” in that it minimizes some mathematical criteria. We present these mathematical criteria in Subsection 29.4.2, but I suggest you read this subsection only after first reading the rest of this section on regression with one numerical explanatory variable.
29.2.2 Simple linear regression
You may recall from secondary/high school algebra that the equation of a line is . (Note that the symbol is equivalent to the “multiply by” mathematical symbol. I’ll typically use the symbol in the rest of this book as it is more succinct—it’s also a helpful reminder that the sign for multiplication in R is *) It is defined by two coefficients: and . The intercept coefficient is the value of when . The slope coefficient for is the increase in for every increase of one in . This is also called the “rise over run.”
However, when defining a regression line like the regression line in Figure 29.5, we tend to use slightly different notation: the equation of the regression line is . The intercept coefficient is , so is the value of when . The slope coefficient for is , i.e., the increase in for every increase of one in . Why do we put a “hat” on top of the ? It’s a form of notation commonly used in regression to indicate that we have a “fitted value,” or the value of on the regression line for a given value. We’ll discuss this more in the upcoming Subsection 29.2.3.
We know that the regression line in Figure 29.5 has a positive slope corresponding to our explanatory variable bty_avg. Why? Because as instructors tend to have higher bty_avg scores, so also do they tend to have higher teaching evaluation scores. However, what is the numerical value of the slope ? What about the intercept ? Let’s not compute these two values by hand, but rather let’s use a computer!
We can obtain the values of the intercept and the slope for bty_avg by outputting a linear regression table. This is done in two steps:
- We first “fit” the linear regression model using the
lm()function and save it inscore_model. - We get the regression table by applying the
get_regression_table()function from themoderndivepackage toscore_model.
# Fit regression model:
score_model <- lm(score ~ bty_avg, data = evals_walkthrough)
# Get regression table:
get_regression_table(score_model)| term | estimate | std_error | statistic | p_value | lower_ci | upper_ci |
|---|---|---|---|---|---|---|
| intercept | 3.880 | 0.076 | 50.96 | 0 | 3.731 | 4.030 |
| bty_avg | 0.067 | 0.016 | 4.09 | 0 | 0.035 | 0.099 |
Let’s first focus on interpreting the regression table output in Table 29.4, and then we’ll later revisit the code that produced it. In the estimate column of Table 29.4 are the intercept = 3.88 and the slope = 0.067 for bty_avg. Thus the equation of the regression line in Figure 29.5 follows:
The intercept = 3.88 is the average teaching score = for those courses where the instructor had a “beauty” score bty_avg of 0. Or in graphical terms, it’s where the line intersects the axis when = 0. Note, however, that while the intercept of the regression line has a mathematical interpretation, it has no practical interpretation here, since observing a bty_avg of 0 is impossible; it is the average of the “beauty” scores ranging from 1 to 10 assigned by six panelists. Furthermore, looking at the scatterplot with the regression line in Figure 29.5, no instructors had a “beauty” score anywhere near 0.
Of greater interest is the slope = for bty_avg of 0.067, as this summarizes the relationship between the teaching and “beauty” score variables. Note that the sign is positive, suggesting a positive relationship between these two variables, meaning teachers with higher “beauty” scores also tend to have higher teaching scores. Recall from earlier that the correlation coefficient is 0.187. They both have the same positive sign, but have a different value. Recall further that the correlation’s interpretation is the “strength of linear association”. The slope’s interpretation is a little different:
For every increase of 1 unit in
bty_avg, there is an associated increase of, on average, 0.067 units ofscore.
We only state that there is an associated increase and not necessarily a causal increase. For example, perhaps it’s not that higher “beauty” scores directly cause higher teaching scores per se. Instead, the following could hold true: individuals from wealthier backgrounds tend to have stronger educational backgrounds and hence have higher teaching scores, while at the same time these wealthy individuals also tend to have higher “beauty” scores. In other words, just because two variables are strongly associated, it doesn’t necessarily mean that one causes the other. This is summed up in the often quoted phrase (which we’ve already seen once this week), “correlation is not necessarily causation.” We’ll discuss this idea further in Subsection 29.4.1.
Furthermore, we say that this associated increase is on average 0.067 units of teaching score, because you might have two instructors whose bty_avg scores differ by 1 unit, but their difference in teaching scores won’t necessarily be exactly 0.067. What the slope of 0.067 is saying is that across all possible courses, the average difference in teaching score between two instructors whose “beauty” scores differ by one is 0.067.
Now that we’ve learned how to compute the equation for the regression line in Figure 29.5 using the values in the estimate column of Table 29.4, and how to interpret the resulting intercept and slope, let’s revisit the code that generated this table:
# Fit regression model:
score_model <- lm(score ~ bty_avg, data = evals_walkthrough)
# Get regression table:
get_regression_table(score_model)First, we “fit” the linear regression model to the data using the lm() function and save this as score_model. When we say “fit”, we mean “find the best fitting line to this data.” lm() stands for “linear model” and is used as follows: lm(y ~ x, data = data_frame_name) where:
yis the outcome variable, followed by a tilde~. In our case,yis set toscore.xis the explanatory variable. In our case,xis set tobty_avg.- The combination of
y ~ xis called a model formula. (Note the order ofyandx.) In our case, the model formula isscore ~ bty_avg. We saw such model formulas earlier when we computed the correlation coefficient using theget_correlation()function in Subsection 29.2.1. data_frame_nameis the name of the data frame that contains the variablesyandx. In our case,data_frame_nameis theevals_walkthroughdata frame.
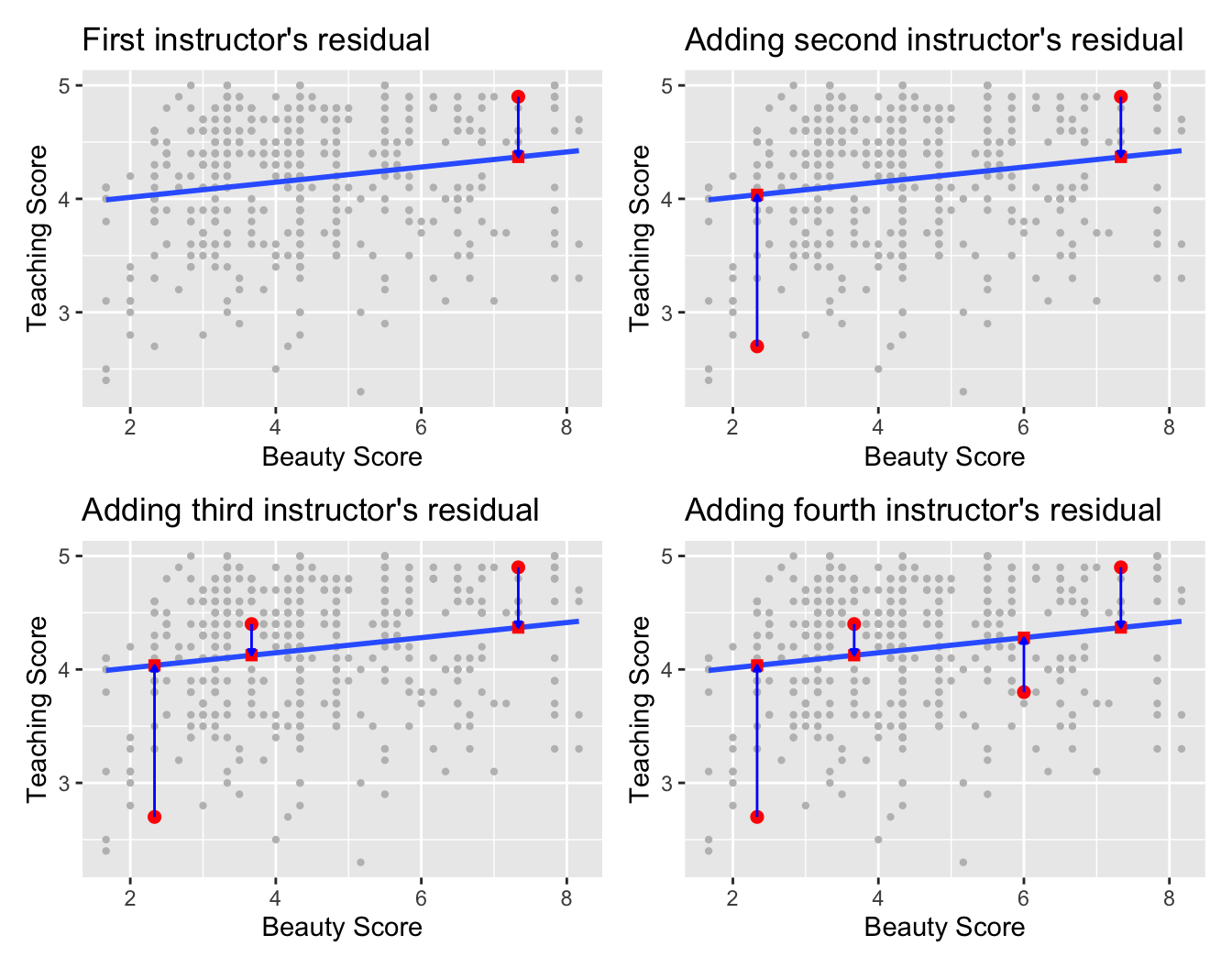
Second, we take the saved model in score_model and apply the get_regression_table() function from the moderndive package to it to obtain the regression table in Table 29.4. This function is an example of what’s known in computer programming as a wrapper function. They take other pre-existing functions and “wrap” them into a single function that hides its inner workings. This concept is illustrated in Figure 29.6.

Figure 29.6: The concept of a wrapper function.
So all you need to worry about is what the inputs look like and what the outputs look like; you leave all the other details “under the hood of the car.” In our regression modeling example, the get_regression_table() function takes a saved lm() linear regression model as input and returns a data frame of the regression table as output. If you’re interested in learning more about the get_regression_table() function’s inner workings, check out Subsection 29.4.3.
Lastly, you might be wondering what the remaining five columns in Table 29.4 are: std_error, statistic, p_value, lower_ci and upper_ci. They are the standard error, test statistic, p-value, lower 95% confidence interval bound, and upper 95% confidence interval bound. They tell us about both the statistical significance and practical significance of our results. This is loosely the “meaningfulness” of our results from a statistical perspective. Let’s put aside these ideas for now and revisit them in Chapter 44 on (statistical) inference for regression. We’ll do this after we’ve had a chance to cover standard errors in Chapter 35, confidence intervals in Chapter 38, and hypothesis testing and -values in Chapter 41.
29.2.3 Observed/fitted values and residuals
We just saw how to get the value of the intercept and the slope of a regression line from the estimate column of a regression table generated by the get_regression_table() function. Now instead say we want information on individual observations. For example, let’s focus on the 21st of the 463 courses in the evals_walkthrough data frame in Table 29.6:
| ID | score | bty_avg | age |
|---|---|---|---|
| 21 | 4.9 | 7.33 | 31 |
What is the value on the regression line corresponding to this instructor’s bty_avg “beauty” score of 7.333? In Figure 29.7 we mark three values corresponding to the instructor for this 21st course and give their statistical names:
- Circle: The observed value = 4.9 is this course’s instructor’s actual teaching score.
- Square: The fitted value is the value on the regression line for =
bty_avg= 7.333. This value is computed using the intercept and slope in the previous regression table:
- Arrow: The length of this arrow is the residual and is computed by subtracting the fitted value from the observed value . The residual can be thought of as a model’s error or “lack of fit” for a particular observation. In the case of this course’s instructor, it is = 4.9 - 4.369 = 0.531.
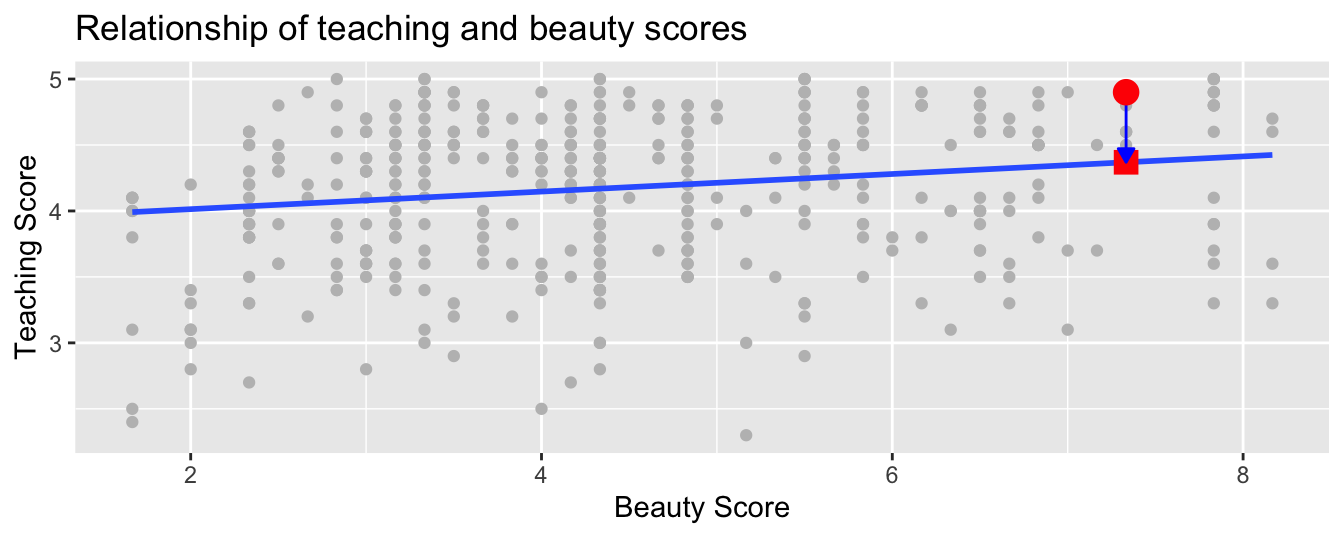
Figure 29.7: Example of observed value, fitted value, and residual.
Now say we want to compute both the fitted value and the residual for all 463 courses in the study. Recall that each course corresponds to one of the 463 rows in the evals_walkthrough data frame and also one of the 463 points in the regression plot in Figure 29.7.
We could repeat the previous calculations we performed by hand 463 times, but that would be tedious and time consuming. Instead, let’s do this using a computer with the get_regression_points() function. Just like the get_regression_table() function, the get_regression_points() function is a “wrapper” function. However, this function returns a different output. Let’s apply the get_regression_points() function to score_model, which is where we saved our lm() model in the previous section. When you run this code, you’ll see all of the output, but in Table 29.8 I’ve presented the results of only the 21st through 24th courses for brevity’s sake.
| ID | score | bty_avg | score_hat | residual |
|---|---|---|---|---|
| 21 | 4.9 | 7.33 | 4.37 | 0.531 |
| 22 | 4.6 | 7.33 | 4.37 | 0.231 |
| 23 | 4.5 | 7.33 | 4.37 | 0.131 |
| 24 | 4.4 | 5.50 | 4.25 | 0.153 |
Let’s inspect the individual columns and match them with the elements of Figure 29.7:
- The
scorecolumn represents the observed outcome variable . This is the y-position of the 463 black points. - The
bty_avgcolumn represents the values of the explanatory variable . This is the x-position of the 463 black points. - The
score_hatcolumn represents the fitted values . This is the corresponding value on the regression line for the 463 values. - The
residualcolumn represents the residuals . This is the 463 vertical distances between the 463 black points and the regression line.
Just as we did for the instructor of the 21st course in the evals_walkthrough dataset (in the first row of the table), let’s repeat the calculations for the instructor of the 24th course (in the fourth row of Table 29.8):
score= 4.4 is the observed teachingscorefor this course’s instructor.bty_avg= 5.50 is the value of the explanatory variablebty_avgfor this course’s instructor.score_hat= 4.25 = 3.88 + 0.067 5.50 is the fitted value on the regression line for this course’s instructor.residual= 0.153 = 4.4 - 4.25 is the value of the residual for this instructor. In other words, the model’s fitted value was off by 0.153 teaching score units for this course’s instructor.
At this point, you can skip ahead if you like to Subsection 29.4.2 to learn about the processes behind what makes “best-fitting” regression lines. As a primer, a “best-fitting” line refers to the line that minimizes the sum of squared residuals out of all possible lines we can draw through the points. In Section 29.3, we’ll discuss another common scenario of having a categorical explanatory variable and a numerical outcome variable.
29.3 One categorical explanatory variable
It’s an unfortunate truth that life expectancy is not the same across all countries in the world. International development agencies are interested in studying these differences in life expectancy in the hopes of identifying where governments should allocate resources to address this problem. In this section, we’ll explore differences in life expectancy in two ways:
- Differences between continents: Are there significant differences in average life expectancy between the five populated continents of the world: Africa, the Americas, Asia, Europe, and Oceania?
- Differences within continents: How does life expectancy vary within the world’s five continents? For example, is the spread of life expectancy among the countries of Africa larger than the spread of life expectancy among the countries of Asia?
To answer such questions, we’ll use the gapminder data frame included in the gapminder package. This dataset has international development statistics such as life expectancy, GDP per capita, and population for 142 countries for 5-year intervals between 1952 and 2007.
We’ll use this data for basic regression but now using an explanatory variable that is categorical, as opposed to the numerical explanatory variable model we used in the previous Section 29.2.
- A numerical outcome variable (a country’s life expectancy) and
- A single categorical explanatory variable (the continent that the country is a part of).
When the explanatory variable is categorical, the concept of a “best-fitting” regression line is a little different than the one we saw previously in Section 29.2 where the explanatory variable was numerical. We’ll study these differences shortly in Subsection 29.3.2, but first we conduct an exploratory data analysis.
29.3.1 Exploratory data analysis
The data on the 142 countries can be found in the gapminder data frame included in the gapminder package. However, to keep things simple, let’s filter() for only those observations/rows corresponding to the year 2007. Additionally, let’s select() only the subset of the variables we’ll consider in this chapter. We’ll save this data in a new data frame called gapminder2007:
library(gapminder)
gapminder2007 <- gapminder %>%
filter(year == 2007) %>%
select(country, lifeExp, continent, gdpPercap)Let’s perform the first common step in an exploratory data analysis: looking at the raw data values. You can do this by using RStudio’s spreadsheet viewer or by using the glimpse() command as introduced in Subsection 8.5.3 on exploring data frames:
Rows: 142
Columns: 4
$ country <fct> "Afghanistan", "Albania", "Algeria", "Angola", "Argentina", …
$ lifeExp <dbl> 43.8, 76.4, 72.3, 42.7, 75.3, 81.2, 79.8, 75.6, 64.1, 79.4, …
$ continent <fct> Asia, Europe, Africa, Africa, Americas, Oceania, Europe, Asi…
$ gdpPercap <dbl> 975, 5937, 6223, 4797, 12779, 34435, 36126, 29796, 1391, 336…Observe that Rows: 142 indicates that there are 142 rows/observations in gapminder2007, where each row corresponds to one country. In other words, the observational unit is an individual country. Furthermore, observe that the variable continent is of type <fct>, which stands for factor, which is R’s way of encoding categorical variables.
A full description of all the variables included in gapminder can be found by reading the associated help file (run ?gapminder in the console). However, let’s fully describe only the 4 variables we selected in gapminder2007:
country: An identification variable of type character/text used to distinguish the 142 countries in the dataset.lifeExp: A numerical variable of that country’s life expectancy at birth. This is the outcome variable of interest.continent: A categorical variable with five levels. Here “levels” correspond to the possible categories: Africa, Asia, Americas, Europe, and Oceania. This is the explanatory variable of interest.gdpPercap: A numerical variable of that country’s GDP per capita in US inflation-adjusted dollars that we’ll use as another outcome variable in the Learning check at the end of this subsection.
Let’s look at a random sample of five out of the 142 countries in Table 29.9 (remember that while you should run this code for practice, you’ll likely get different numbers).
| country | lifeExp | continent | gdpPercap |
|---|---|---|---|
| Togo | 58.4 | Africa | 883 |
| Sao Tome and Principe | 65.5 | Africa | 1598 |
| Congo, Dem. Rep. | 46.5 | Africa | 278 |
| Lesotho | 42.6 | Africa | 1569 |
| Bulgaria | 73.0 | Europe | 10681 |
Now that we’ve looked at the raw values in our gapminder2007 data frame and got a sense of the data, let’s move on to computing summary statistics. Let’s once again apply the skim() function from the skimr package. Recall from our previous EDA that this function takes in a data frame, “skims” it, and returns commonly used summary statistics. Let’s take our gapminder2007 data frame, select() only the outcome and explanatory variables lifeExp and continent, and pipe them into the skim() function:
| Name | Piped data |
| Number of rows | 142 |
| Number of columns | 2 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 1 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| continent | 0 | 1 | FALSE | 5 | Afr: 52, Asi: 33, Eur: 30, Ame: 25 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| lifeExp | 0 | 1 | 67 | 12.1 | 39.6 | 57.2 | 71.9 | 76.4 | 82.6 | ▂▃▃▆▇ |
The skim() output now reports summaries for categorical variables (Variable type:factor) separately from the numerical variables (Variable type:numeric). For the categorical variable continent, it reports:
n_missingandcomplete_rate, which, as before, are the number of missing values and the proportion of complete values respectively.n_unique: The number of unique levels to this variable. Since we’re working with continents, and this dataset recognizes 5 different continents, that’s the number we get,corresponding to Africa, Asia, Americas, Europe, and Oceania.top_counts: In this case, the top four counts:Africahas 52 countries,Asiahas 33,Europehas 30, andAmericashas 25. Not displayed isOceaniawith 2 countries.
Turning our attention to the summary statistics of the numerical variable lifeExp, we observe that the global median life expectancy in 2007 was 71.94. Thus, half of the world’s countries (71 countries) had a life expectancy less than 71.94. The mean life expectancy of 67.01 is lower, however. Why is the mean life expectancy lower than the median?
We can answer this question by performing the last of the three common steps in an exploratory data analysis: creating data visualizations. Let’s visualize the distribution of our outcome variable = lifeExp in Figure 29.8.
ggplot(gapminder2007, aes(x = lifeExp)) +
geom_histogram(binwidth = 5, color = "white") +
labs(x = "Life expectancy", y = "Number of countries",
title = "Histogram of distribution of worldwide life expectancies")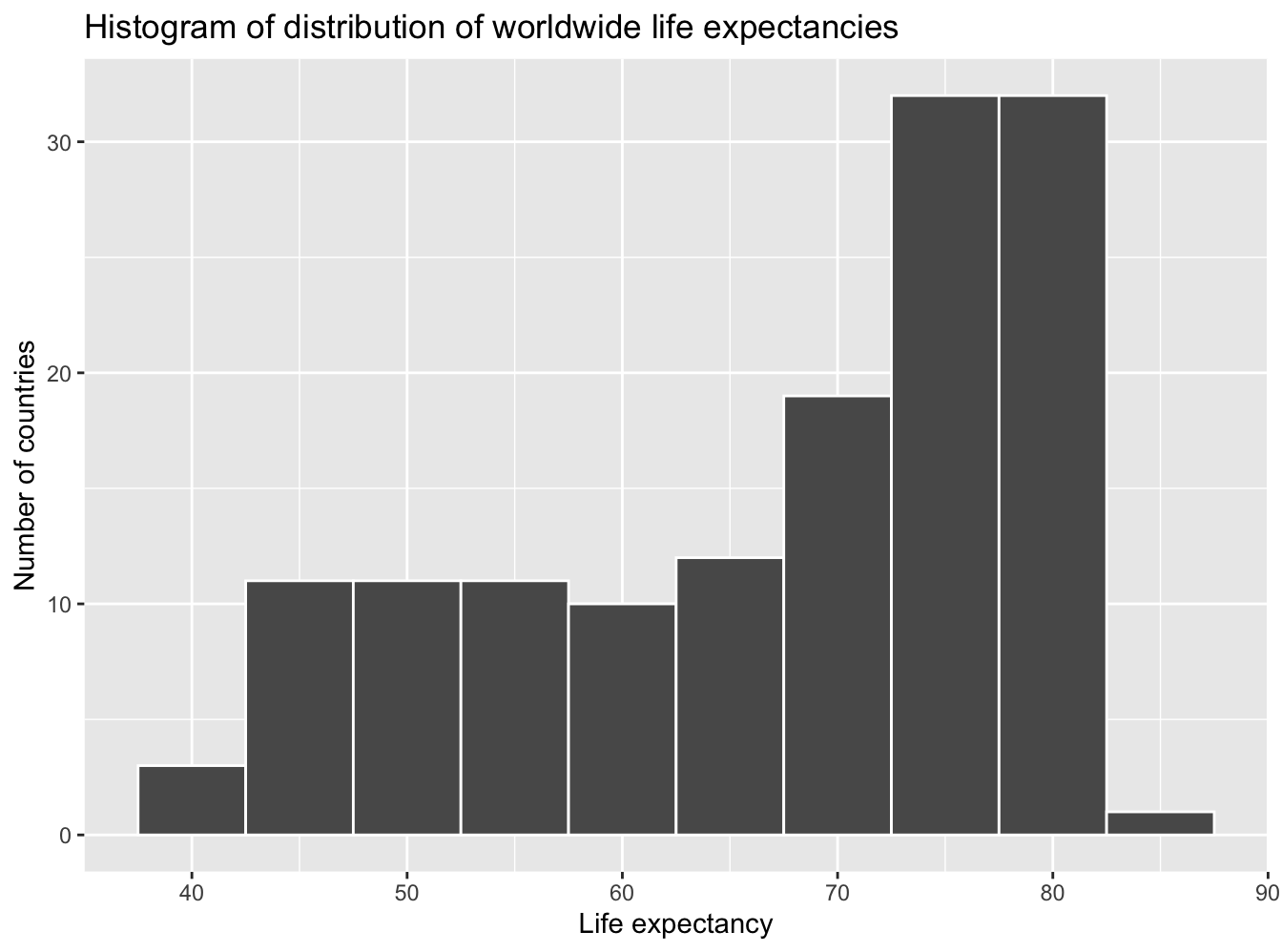
Figure 29.8: Histogram of life expectancy in 2007.
We see that this data is left-skewed, also known as negatively skewed: there are a few countries with low life expectancy that are bringing down the mean life expectancy. However, the median is less sensitive to the effects of such outliers; hence, the median is greater than the mean in this case.
Remember, however, that we want to compare life expectancies both between continents and within continents. In other words, our visualizations need to incorporate some notion of the variable continent. We can do this easily with a faceted histogram. Recall from Section 23.7 that facets allow us to split a visualization by the different values of another variable. We display the resulting visualization in Figure 29.9 by adding a facet_wrap(~ continent, nrow = 2) layer.
ggplot(gapminder2007, aes(x = lifeExp)) +
geom_histogram(binwidth = 5, color = "white") +
labs(x = "Life expectancy",
y = "Number of countries",
title = "Histogram of distribution of worldwide life expectancies") +
facet_wrap(~ continent, nrow = 2)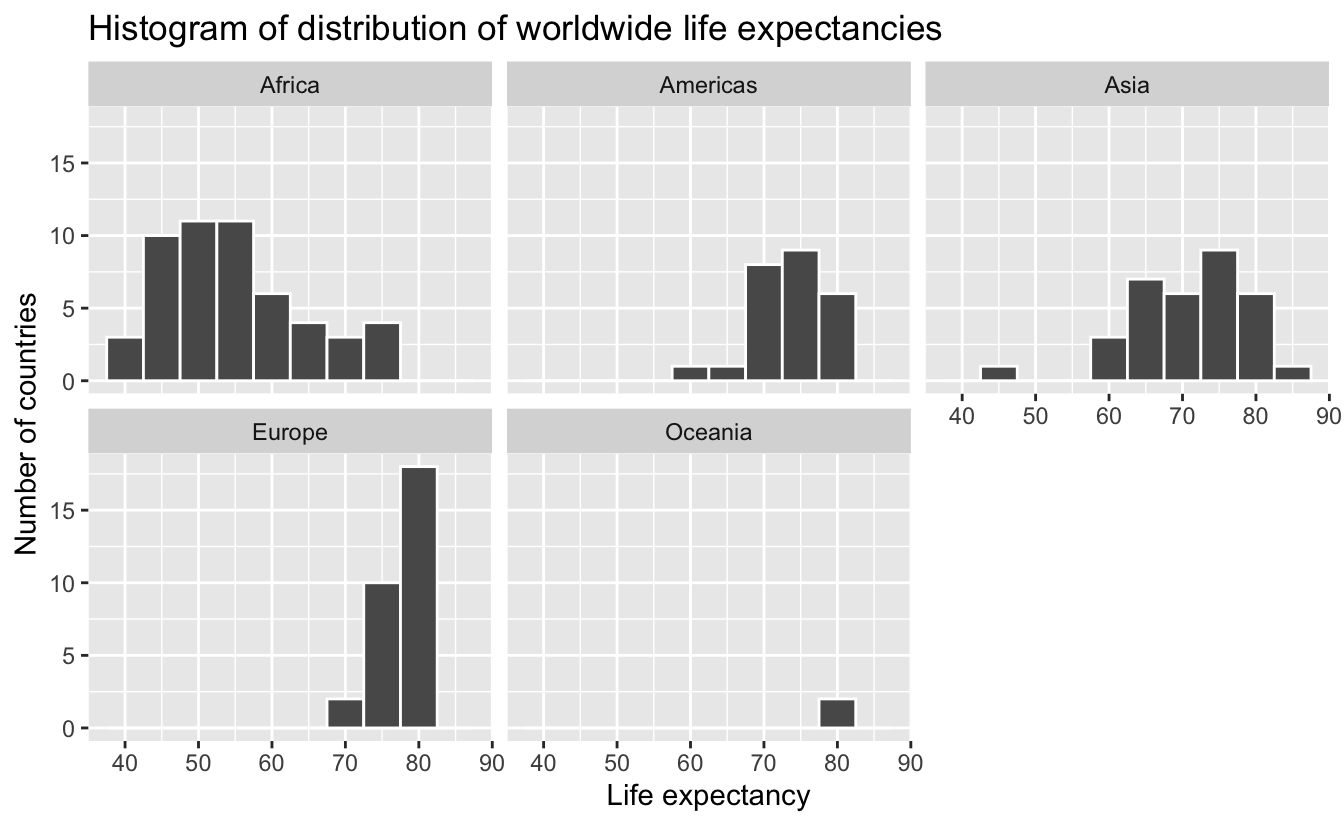
Figure 29.9: Life expectancy in 2007.
Observe that the distribution of African life expectancies is unfortunately much lower than the other continents. In contrast, life expectancies in Europe tend to be higher—and, furthermore, do not vary as much. On the other hand, both Asia and Africa have the most variation in life expectancies. There is the least variation in Oceania, but keep in mind that there are only two countries in Oceania: Australia and New Zealand.
Recall that an alternative method to visualize the distribution of a numerical variable split by a categorical variable is by using a side-by-side boxplot. We map the categorical variable continent to the -axis and the different life expectancies within each continent on the -axis in Figure 29.10.
ggplot(gapminder2007, aes(x = continent, y = lifeExp)) +
geom_boxplot() +
labs(x = "Continent", y = "Life expectancy",
title = "Life expectancy by continent")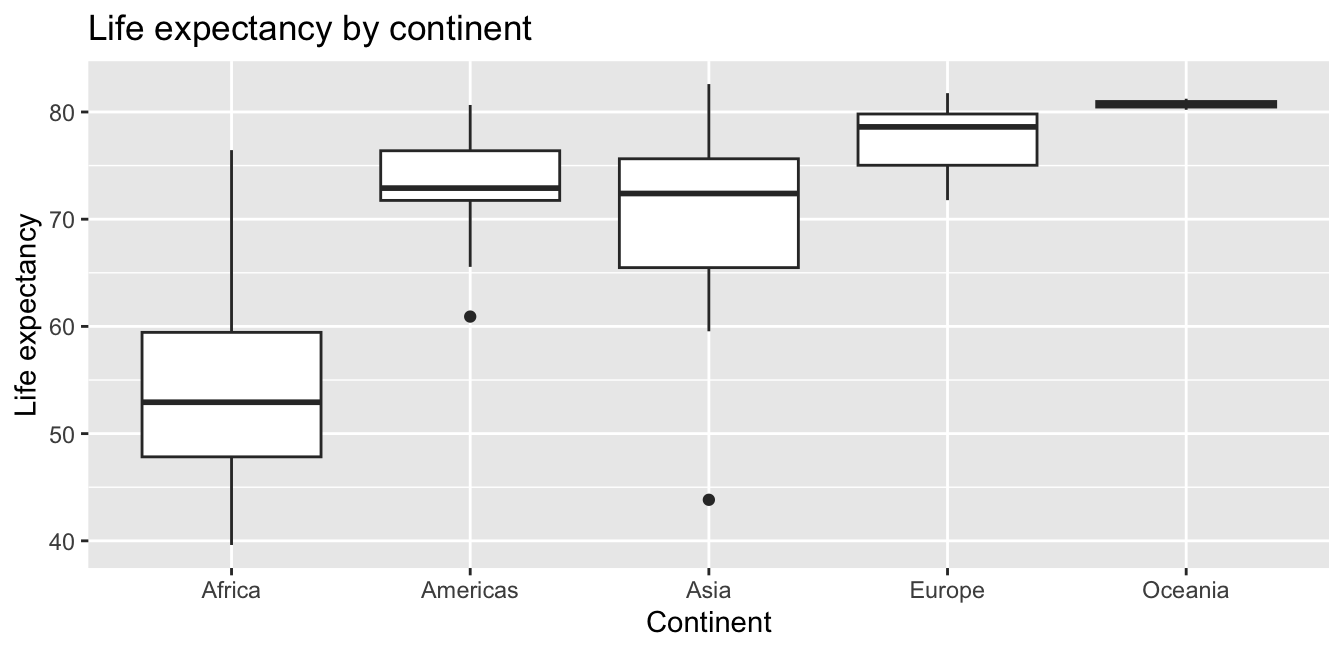
Figure 29.10: Life expectancy in 2007.
Some people prefer comparing the distributions of a numerical variable between different levels of a categorical variable using a boxplot instead of a faceted histogram. This is because we can make quick comparisons between the categorical variable’s levels with imaginary horizontal lines. For example, observe in Figure 29.10 that we can quickly convince ourselves that Oceania has the highest median life expectancies by drawing an imaginary horizontal line at = 80. Furthermore, as we observed in the faceted histogram in Figure 29.9, Africa and Asia have the largest variation in life expectancy as evidenced by their large interquartile ranges (the heights of the boxes).
It’s important to remember, however, that the solid lines in the middle of the boxes correspond to the medians (the middle value) rather than the mean (the average). So, for example, if you look at Asia, the solid line denotes the median life expectancy of around 72 years. This tells us that half of all countries in Asia have a life expectancy below 72 years, whereas half have a life expectancy above 72 years.
Let’s compute the median and mean life expectancy for each continent with a little more data wrangling and display the results in Table 29.12.
lifeExp_by_continent <- gapminder2007 %>%
group_by(continent) %>%
summarize(median = median(lifeExp),
mean = mean(lifeExp))
lifeExp_by_continent| continent | median | mean |
|---|---|---|
| Africa | 52.9 | 54.8 |
| Americas | 72.9 | 73.6 |
| Asia | 72.4 | 70.7 |
| Europe | 78.6 | 77.6 |
| Oceania | 80.7 | 80.7 |
Observe the order of the second column median life expectancy: Africa is lowest, the Americas and Asia are next with similar medians, then Europe, then Oceania. This ordering corresponds to the ordering of the solid black lines inside the boxes in our side-by-side boxplot in Figure 29.10.
Let’s now turn our attention to the values in the third column mean. Using Africa’s mean life expectancy of 54.8 as a baseline for comparison, let’s start making comparisons to the mean life expectancies of the other four continents and put these values in Table 29.13, which we’ll revisit later on in this section.
- For the Americas, it is 73.6 - 54.8 = 18.8 years higher.
- For Asia, it is 70.7 - 54.8 = 15.9 years higher.
- For Europe, it is 77.6 - 54.8 = 22.8 years higher.
- For Oceania, it is 80.7 - 54.8 = 25.9 years higher.
| continent | mean | Difference versus Africa |
|---|---|---|
| Africa | 54.8 | 0.0 |
| Americas | 73.6 | 18.8 |
| Asia | 70.7 | 15.9 |
| Europe | 77.6 | 22.8 |
| Oceania | 80.7 | 25.9 |
29.3.2 Linear regression
In Subsection 29.2.2 we introduced simple linear regression, which involves modeling the relationship between a numerical outcome variable and a numerical explanatory variable . In our life expectancy example, we now instead have a categorical explanatory variable continent. Our model will not yield a “best-fitting” regression line like in Figure 29.5, but rather offsets relative to a baseline for comparison.
As we did in Subsection 29.2.2 when studying the relationship between teaching scores and “beauty” scores, let’s output the regression table for this model. Recall that this is done in two steps:
- We first “fit” the linear regression model using the
lm(y ~ x, data)function and save it inlifeExp_model. - We get the regression table by applying the
get_regression_table()function from themoderndivepackage tolifeExp_model.
| term | estimate | std_error | statistic | p_value | lower_ci | upper_ci |
|---|---|---|---|---|---|---|
| intercept | 54.8 | 1.02 | 53.45 | 0 | 52.8 | 56.8 |
| continent: Americas | 18.8 | 1.80 | 10.45 | 0 | 15.2 | 22.4 |
| continent: Asia | 15.9 | 1.65 | 9.68 | 0 | 12.7 | 19.2 |
| continent: Europe | 22.8 | 1.70 | 13.47 | 0 | 19.5 | 26.2 |
| continent: Oceania | 25.9 | 5.33 | 4.86 | 0 | 15.4 | 36.5 |
Let’s once again focus on the values in the term and estimate columns of Table 29.15. Why are there now 5 rows? Let’s break them down one-by-one:
interceptcorresponds to the mean life expectancy of countries in Africa of 54.8 years.continent: Americascorresponds to countries in the Americas and the value +18.8 is the same difference in mean life expectancy relative to Africa we displayed in Table 29.13. In other words, the mean life expectancy of countries in the Americas is .continent: Asiacorresponds to countries in Asia and the value +15.9 is the same difference in mean life expectancy relative to Africa we displayed in Table 29.13. In other words, the mean life expectancy of countries in Asia is .continent: Europecorresponds to countries in Europe and the value +22.8 is the same difference in mean life expectancy relative to Africa we displayed in Table 29.13. In other words, the mean life expectancy of countries in Europe is .continent: Oceaniacorresponds to countries in Oceania and the value +25.9 is the same difference in mean life expectancy relative to Africa we displayed in Table 29.13. In other words, the mean life expectancy of countries in Oceania is .
To summarize, the 5 values in the estimate column in Table 29.15 correspond to the “baseline for comparison” continent Africa (the intercept) as well as four “offsets” from this baseline for the remaining 4 continents: the Americas, Asia, Europe, and Oceania.
You might be asking at this point why was Africa chosen as the “baseline for comparison” group. This is the case for no other reason than it comes first alphabetically of the five continents; by default R arranges factors/categorical variables in alphanumeric order. You can change this baseline group to be another continent if you manipulate the variable continent’s factor “levels” using the forcats package. See Chapter 15 of R for Data Science (Grolemund & Wickham, 2017) for examples.
Let’s now write the equation for our fitted values .
Whoa! That looks daunting! Don’t fret, however, as once you understand what all the elements mean, things simplify greatly. First, is what’s known in mathematics as an “indicator function.” It returns only one of two possible values, 0 and 1, where
In a statistical modeling context, this is also known as a dummy variable. In our case, let’s consider the first such indicator variable . This indicator function returns 1 if a country is in the Americas, 0 otherwise:
Second, corresponds to the intercept as before; in this case, it’s the mean life expectancy of all countries in Africa. Third, the , , , and represent the 4 “offsets relative to the baseline for comparison” in the regression table output in Table 29.15: continent: Americas, continent: Asia, continent: Europe, and continent: Oceania.
Let’s put this all together and compute the fitted value for a country in Africa. Since the country is in Africa, all four indicator functions , , , and will equal 0, and thus:
In other words, all that’s left is the intercept , corresponding to the average life expectancy of African countries of 54.8 years. Next, say we are considering a country in the Americas. In this case, only the indicator function for the Americas will equal 1, while all the others will equal 0, and thus:
which is the mean life expectancy for countries in the Americas of 73.6 years in Table 29.13. Note the “offset from the baseline for comparison” is +18.8 years.
Let’s do one more. Say we are considering a country in Asia. In this case, only the indicator function for Asia will equal 1, while all the others will equal 0, and thus:
which is the mean life expectancy for Asian countries of 70.7 years in Table 29.13. The “offset from the baseline for comparison” here is +15.9 years.
Let’s generalize this idea a bit. If we fit a linear regression model using a categorical explanatory variable that has possible categories, the regression table will return an intercept and “offsets.” In our case, since there are continents, the regression model returns an intercept corresponding to the baseline for comparison group of Africa and offsets corresponding to the Americas, Asia, Europe, and Oceania.
Understanding a regression table output when you’re using a categorical explanatory variable is a topic those new to regression often struggle with. The only real remedy for these struggles is practice, practice, practice. However, once you equip yourselves with an understanding of how to create regression models using categorical explanatory variables, you’ll be able to incorporate many new variables into your models, given the large amount of the world’s data that is categorical. If you feel like you’re still struggling at this point, however, I suggest you closely compare Tables 29.13 and 29.15 and note how you can compute all the values from one table using the values in the other.
29.3.3 Observed/fitted values and residuals
Recall in Subsection 29.2.3, we defined the following three concepts:
- Observed values , or the observed value of the outcome variable
- Fitted values , or the value on the regression line for a given value
- Residuals , or the error between the observed value and the fitted value
We obtained these values and other values using the get_regression_points() function from the moderndive package. This time, however, let’s add an argument setting ID = "country": this is telling the function to use the variable country in gapminder2007 as an identification variable in the output. This will help contextualize our analysis by matching values to countries.
| country | lifeExp | continent | lifeExp_hat | residual |
|---|---|---|---|---|
| Afghanistan | 43.8 | Asia | 70.7 | -26.900 |
| Albania | 76.4 | Europe | 77.6 | -1.226 |
| Algeria | 72.3 | Africa | 54.8 | 17.495 |
| Angola | 42.7 | Africa | 54.8 | -12.075 |
| Argentina | 75.3 | Americas | 73.6 | 1.712 |
| Australia | 81.2 | Oceania | 80.7 | 0.516 |
| Austria | 79.8 | Europe | 77.6 | 2.180 |
| Bahrain | 75.6 | Asia | 70.7 | 4.907 |
| Bangladesh | 64.1 | Asia | 70.7 | -6.666 |
| Belgium | 79.4 | Europe | 77.6 | 1.792 |
Observe in Table 29.17 that lifeExp_hat contains the fitted values = . If you look closely, there are only 5 possible values for lifeExp_hat. These correspond to the five mean life expectancies for the 5 continents that we displayed in Table 29.13 and computed using the values in the estimate column of the regression table in Table 29.15.
The residual column is simply = lifeExp - lifeExp_hat. These values can be interpreted as the deviation of a country’s life expectancy from its continent’s average life expectancy. For example, look at the first row of Table 29.17 corresponding to Afghanistan. The residual of is telling us that Afghanistan’s life expectancy is a whopping 26.9 years lower than the mean life expectancy of all Asian countries. This can in part be explained by the many years of war that country has suffered.
29.5 Conclusion
In this chapter, you’ve studied the term basic regression, where you fit models that only have one explanatory variable. In Chapter 32, we’ll study multiple regression, where our regression models can now have more than one explanatory variable! In particular, we’ll consider two scenarios: regression models with one numerical and one categorical explanatory variable and regression models with two numerical explanatory variables. This will allow you to construct more sophisticated and more powerful models, all in the hopes of better explaining your outcome variable .